Nous expliquons ce qu’est l’algèbre, son histoire, ses branches et à quoi elle sert. Aussi, le langage et les expressions algébriques.

Qu’est-ce que l’algèbre ?
L’algèbre est l’une des principales branches des mathématiques . Son objet d’étude sont des structures abstraites opérant dans des modèles fixes, à l’intérieur desquels il y a généralement plus que des nombres et des opérations arithmétiques : aussi des lettres, qui représentent des opérations concrètes, des variables , des inconnues ou des coefficients.
Plus simplement, c’est la branche des mathématiques qui traite des opérations avec et entre les symboles , généralement représentés par des lettres. Son nom vient de l’arabe al-jabr (« réintégration » ou « recomposition »).
L’algèbre est l’une des branches des mathématiques avec les plus grandes applications. Il permet de représenter les problèmes formels de la vie quotidienne. Par exemple, des équations et des variables algébriques permettent de calculer des proportions inconnues .
La logique , la reconnaissance des formes et le raisonnement inductif et déductif sont quelques-unes des capacités mentales qu’il requiert, favorise et développe.
Voir aussi: Pensée mathématique
histoire de l’algèbre

L’algèbre est née dans la culture arabe, vers l’an 820 après JC. C. , date à laquelle fut publié le premier traité sur la question : Al-kitāb al-mukhtaṣar fī ḥisāb al-ŷarabi waˀl-muqābala , c’est-à-dire « Compendium de calcul par réintégration et comparaison », ouvrage du mathématicien persan et l’astronome Muhammad ibn Musa al-Jwarizmi, connu sous le nom d’Al Juarismi.
Là, le sage a offert la solution systématique des équations linéaires et quadratiques, en utilisant des opérations symboliques. Ces méthodes se sont développées plus tard dans les mathématiques de l’islam médiéval et ont fait de l’algèbre une discipline mathématique distincte , aux côtés de l’arithmétique et de la géométrie.
Ces études ont finalement trouvé leur chemin vers l’Occident. Grâce à eux , l’algèbre abstraite est née au XIXe siècle , basée sur la consolidation des nombres complexes au cours des siècles précédents, fruit de penseurs tels que Gabriel Cramer (1704-1752), Leonhard Euler (1707-1783) et Adrien-Marie Legendre. (1752-1833).
A quoi sert l’algèbre ?
L’algèbre est extrêmement utile dans le domaine des mathématiques, mais elle a aussi de grandes applications dans la vie quotidienne. Il permet de réaliser des budgets , des facturations, des calculs de coûts , de bénéfices et de profits .
De plus, d’autres opérations d’importance dans la comptabilité , l’ administration et même l’ingénierie, sont basées sur des calculs algébriques qui manipulent une ou plusieurs variables, les exprimant dans des relations logiques et des modèles détectables.
L’utilisation de l’algèbre permet aux individus de mieux gérer des concepts complexes et abstraits , en les exprimant de manière plus simple et plus ordonnée grâce à la notation algébrique.
branches de l’algèbre
Les principales ramifications de l’algèbre sont au nombre de deux :
- algèbre élémentaire. Comme son nom l’indique, il comprend les préceptes les plus élémentaires du sujet, introduisant dans les opérations arithmétiques une série de lettres (symboles) qui représentent des quantités ou des relations inconnues. Il s’agit, fondamentalement, de la manipulation d’équations et de variables, d’inconnues, de coefficients, d’indices ou de racines.
- algèbre abstraite. Aussi appelée algèbre moderne, elle représente un degré de complexité plus élevé par rapport à l’algèbre élémentaire, puisqu’elle est dédiée à l’étude des structures algébriques ou des systèmes algébriques, qui sont des ensembles d’opérations associables à des éléments d’un groupe de motifs reconnaissable.
Langage algébrique
L’algèbre exige avant tout une façon propre de nommer ses énoncés, différente du langage arithmétique (composé uniquement de nombres et de symboles), faisant appel à des relations, des variables et des opérations traditionnelles et complexes.
C’est un langage plus synthétique que l’arithmétique, qui permet d’exprimer des relations générales par de brefs énoncés . Elle permet aussi d’inclure dans le schéma formel les termes que l’on ne connaît pas encore (les variables) mais dont le lien avec le reste est connu.
C’est ainsi que surgissent, par exemple, des équations dont la forme de résolution implique le réarrangement des termes algébriques pour « effacer » l’inconnu.
Expressions algébriques
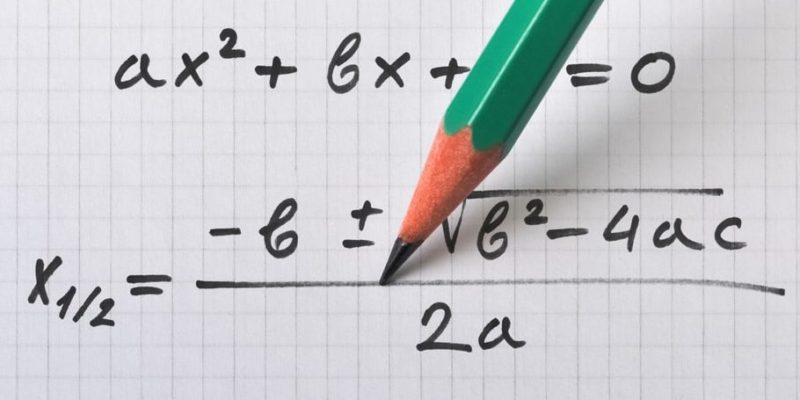
Les expressions algébriques sont la manière d’écrire le langage algébrique . On y reconnaîtra des nombres et des lettres (variables), mais aussi d’autres types de signes, et d’arrangements, tels que des coefficients (chiffres devant une variable), des degrés (exposants) et les signes arithmétiques usuels. En général, les expressions algébriques peuvent être classées en deux :
- Monômes. Une seule expression algébrique, qui contient en elle-même toutes les informations nécessaires pour la résoudre. Par exemple : 6X 2 + 32y 4 .
- Polynômes. Chaînes d’expressions algébriques, c’est-à-dire chaînes de monômes, qui ont une signification globale et doivent être résolues ensemble. Par exemple : 3n5y 3 +23n 5 y8z 3 – π 2 3n – 22 + 26n 4 .
Continuer avec : Géométrie analytique







