Nous expliquons ce qu’est le nombre d’or, son histoire et le nombre d’or. Aussi, le nombre d’or dans la nature et dans l’art.

Quel est le nombre d’or ?
On l’appelle le nombre d’or, la proportion divine, la section dorée ou le nombre d’or, mais aussi le nombre d’or ou le rectangle d’or, entre autres noms, à un élément mathématique dont la présence dans les œuvres artistiques , architecturales et même dans les objets de la nature , explique soi-disant sa beauté.
Pour comprendre ce qu’est le nombre d’or, il faut d’abord comprendre le nombre d’or, un nombre algébrique irrationnel, représenté par la lettre grecque phi (ϕ) en l’honneur du sculpteur grec Phidias (500-431 av. J.-C.), bien que parfois aussi avec tau (Τ) ou encore avec alpha minuscule (α), équivalent à 1,618033988749894… et à (1 + √5) / 2.
Ce nombre a des propriétés mathématiques intéressantes et a été découvert dans l’Antiquité , mais pas comme une expression arithmétique, mais comme une expression géométrique : c’est le rapport ou la proportion entre deux segments d’une droite a et b, qui respectent l’équation algébrique :
(a + b) / a = a / b.
Cette relation s’appelle le nombre d’or.
Depuis lors, les êtres humains ont trouvé cette proportion dans des objets très différents dans la nature, des feuilles des arbres aux carapaces des tortues . On le voit également dans diverses œuvres artistiques et architecturales. On lui a même accordé une certaine importance mystique à travers l’histoire.
Voir aussi : Esthétique
Histoire du nombre d’or
Selon quelques interprétations des découvertes archéologiques, dans les cultures mésopotamiennes du 2000 À. C. il existe déjà des preuves de l’utilisation du nombre d’or, malgré le fait qu’il n’existe aucune documentation antérieure à la Grèce antique dans laquelle on en parle.
Les premières études formelles du nombre d’or appartiennent au philosophe Euclide (c. 300-265 av. J.-C.) , dans son livre Les Éléments , où il est montré qu’il s’agit d’un nombre irrationnel, et quelques autres sont attribuées à Platon lui-même (c. 428-347 av. J.-C.).
En 1509, le théologien et mathématicien italien Luca Pacioli (c. 1445-1517) a suggéré la connexion divine de ce nombre dans son De divina proportione (« Sur la proportion divine »). Pacioli a soutenu qu’il était défini par trois segments droits comme la Trinité divine, qu’il était incompréhensible dans son intégralité comme Dieu, et avait d’autres caractéristiques interprétables comme métaphore du sacré.
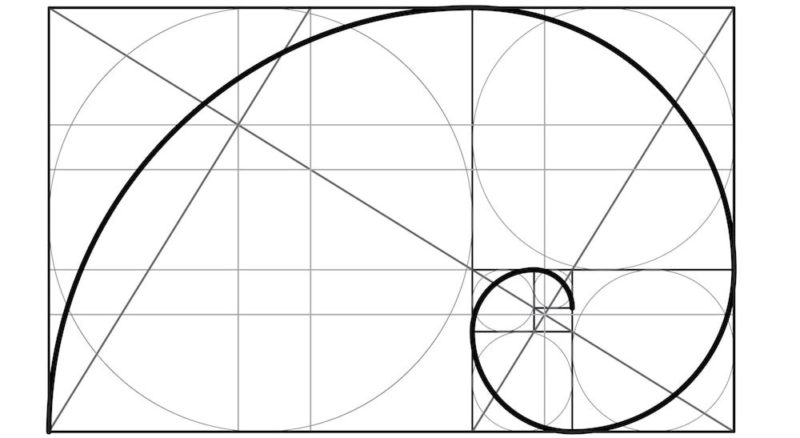
Indubitablement influencé par cette idée, l’artiste allemand de la Renaissance Albrecht Dürer (1471-1528) a conçu la spirale dorée en 1525 , appelée plus tard « spirale de Dürer » : l’artiste a décrit comment dessiner une spirale dorée en se basant sur la proportion divine.
Il existe d’autres références au nombre d’or dans les œuvres de Johannes Kepler (1571-1630) et de Martin Ohm (1792-1872), ce dernier ayant inventé le nom de « nombre d’or » en 1835. Cependant, il existe des preuves que le nom était en usage courant déjà à cette époque.
Depuis lors, elle était représentée par la lettre grecque tau , jusqu’à ce qu’en 1900 le mathématicien Mark Barr la remplace par phi , en hommage au sculpteur grec Phidias.
Nombre d’or dans la nature

Voici quelques exemples de découverte de la section dorée dans la nature :
- La spirale logarithmique à l’intérieur des coquilles d’ animaux marins appelés nautiles.
- L’arrangement des pétales de nombreuses fleurs , selon la loi de Ludwig.
- La relation entre les nervures des feuilles de la plupart des arbres.
- Le nombre de verticilles présentes dans l’écorce d’un ananas .
- La distance entre le nombril et les pieds de toute personne , par rapport à sa taille totale.
- L’arrangement des feuilles d’artichauts .
Nombre d’or dans l’art

Selon certains érudits, plus une œuvre se rapproche du nombre d’or, plus elle sera belle, ou plus elle se rapprochera de la beauté ultime. Il n’y a aucune preuve scientifique de cela, mais il est vrai que le nombre d’or peut être trouvé dans les œuvres artistiques, sculpturales ou architecturales suivantes :
- Dans les relations entre les formes de la Grande Pyramide de Gizeh , selon les thèses d’Hérodote dans ses Historiae .
- La relation entre les parties, les colonnes et le toit de l’ancien temple grec connu sous le nom de Parthénon à Athènes .
- Dans les structures formelles des sonates de Wolfgang Amadeus Mozart , ainsi que dans la Cinquième Symphonie de Beethoven, et plus tard dans des œuvres de Schubert et Debussy.
- Dans le tableau Atomic Leda (1949) du peintre surréaliste Salvador Dalí.
- Dans la structure temporelle des films Battleship Potemkin (1925) et Ivan le Terrible (1944) du cinéaste soviétique Sergei Eisenstein.
- Le mouvement pictural italien de l’ Arte Povera a basé ses peintures sur la succession des nombres de Fibonacci, qui incarnent le nombre d’or.
Continuer avec : Échelle







