Nous expliquons ce que sont les nombres naturels et certaines de leurs caractéristiques. Le plus grand commun diviseur et le plus petit commun multiple.

Que sont les nombres naturels ?
Les nombres naturels sont les nombres qui, dans l’ histoire de l’homme, ont d’abord été utilisés pour compter des objets , non seulement pour les comptabiliser mais aussi pour les ordonner. Ces nombres commencent à partir du chiffre 1. Il n’y a pas de quantité totale ou finale de nombres naturels, ils sont infinis.
Les nombres naturels sont : 1, 2, 3, 4, 5, 6, 7, 8, 9, 10… etc. Comme on peut le voir, ces nombres n’admettent pas de fractions (décimales). Il convient de noter que le nombre zéro est parfois considéré comme un nombre naturel , mais généralement ce n’est pas le cas.
D’autre part, on dit que les nombres naturels ont toujours un nombre successeur. Et les nombres naturels ne font pas de distinction entre les nombres pairs et impairs , ils les incluent tous. Ils n’acceptent pas les fractions ou les nombres négatifs. Ils se distinguent des nombres entiers, car les nombres entiers comprennent également des nombres négatifs. Quant à l’expression écrite des nombres naturels, ceux-ci sont représentés par la lettre N, en majuscules.
Les nombres naturels sont également la base principale sur laquelle reposent toutes les opérations et fonctions mathématiques , addition, soustraction, multiplication et division. Aussi aux fonctions et équations trigonométriques. En bref, ce sont les éléments de base sans lesquels les mathématiques ne pourraient pas exister, d’ailleurs toutes les sciences qui utilisent ce type de calculs comme la géométrie, l’ingénierie, la chimie , la physique , ont toutes besoin de mathématiques et de nombres naturels.
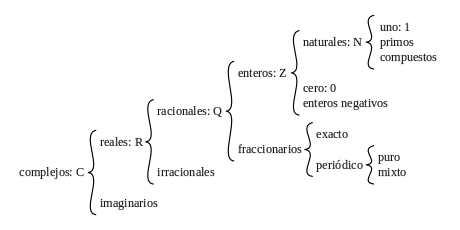 >
>- Le plus grand facteur commun. C’est le plus grand nombre naturel qui a la capacité mathématique de diviser chacun des nombres donnés. Pour trouver ce nombre, il faut d’abord décomposer le nombre en nombres premiers, choisir uniquement les facteurs communs avec le plus petit exposant, et calculer le produit des facteurs.
- Le plus petit commun multiple. C’est le plus petit nombre naturel multiple de chacun des nombres donnés dans une distribution particulière . Et ses étapes pour le trouver consistent à décomposer le nombre en nombres premiers, à choisir les facteurs premiers avec le plus grand exposant, puis à calculer le produit de ces facteurs.
On distingue principalement deux utilisations fondamentales, d’une part pour décrire la position occupée par un certain élément dans une séquence ordonnée , et pour spécifier la taille d’un ensemble fini, qui à son tour est généralisé dans le concept de nombre cardinal (théorie des ensembles). Et deuxièmement, l’autre utilisation de grande importance est celle de la construction mathématique des nombres entiers.
L’ordre des nombres naturels dans une opération donnée ne modifie pas le résultat , c’est ce qu’on appelle la « propriété commutative » des nombres naturels.
Cela peut vous aider : Entiers