Nous expliquons ce qu’est un périmètre, comment il est calculé dans différentes figures géométriques et ses applications dans d’autres disciplines.

Quel est le périmètre ?
En géométrie, le périmètre est la somme des longueurs des côtés de toute figure géométrique plane . C’est un concept clé pour les mathématiques , qui avec le concept d’aire, qui lui est proche, est nécessaire à maîtriser pour s’orienter vers des mathématiques plus avancées comme l’ algèbre et la trigonométrie , puisqu’elles permettent la construction de polygones.
Le mot périmètre vient du grec ancien (union des mots peri , « tout », et métron , « mesurer »), puisque les anciens philosophes grecs ont été les premiers à le calculer . La première de ces pensées est attribuée au philosophe Archimède (vers 287-212 av. J.-C.).
Le concept s’applique à la fois à la distance et à la longueur, ou au tracé des figures ; mais dans le cas des cercles, on l’appelle circonférence . La moitié du périmètre s’appelle le demi-périmètre. Le périmètre est représenté par la lettre P.
Cela peut vous aider à : Pensée mathématique
Applications périmétriques pratiques

Le calcul de périmètre a de nombreuses applications pratiques, en particulier pour l’architecture , l’ingénierie et les travaux de construction . Par exemple, il peut être utilisé pour calculer les bords ou la bordure d’un espace ou d’un objet, comme un terrain ou un bâtiment.
Si nous voulons, par exemple, placer une clôture autour de notre jardin, il faudra calculer le périmètre de sa surface, savoir combien de matériaux acheter et comment les placer.
périmètre d’un cercle
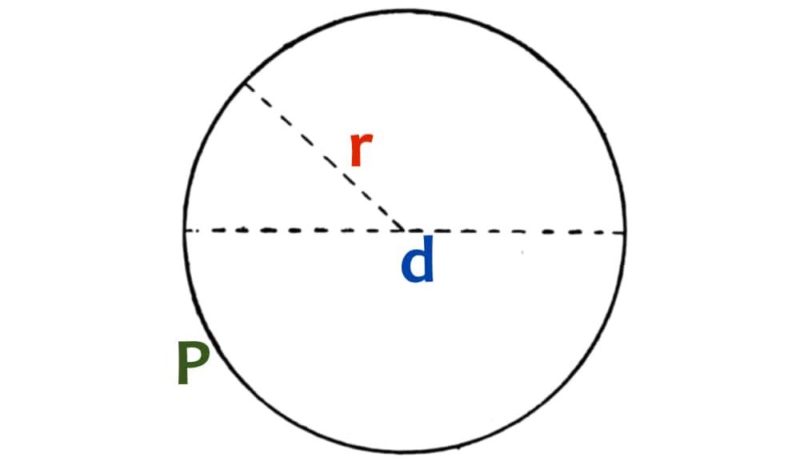
Le périmètre d’un cercle s’appelle la circonférence et se calcule en appliquant la formule suivante :
P = 2π. r = dπ
Où π est la constante mathématique équivalente à 3,14159…, r est la longueur du rayon du cercle et d est la longueur de son diamètre. Dans le cas d’un demi-cercle, la formule devient :
P = 2r + r. π = r(2 + π)
périmètre d’un rectangle
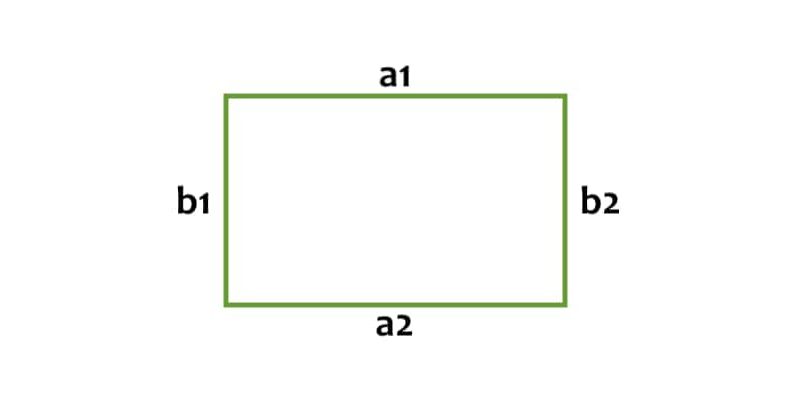
Dans le cas d’un rectangle, il ne sera pas nécessaire de calculer le périmètre plus qu’en additionnant les longueurs de ses deux grands côtés et de ses deux petits côtés . Autrement dit, si le rectangle a deux côtés a (a1, a2) et deux côtés b (b1, b2), le périmètre sera calculé en ajoutant a1 + a2 + b1 + b2.
périmètre d’un carré
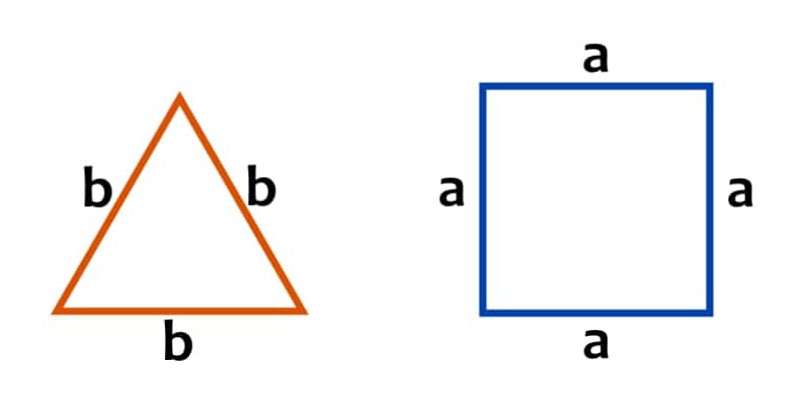
Le cas des carrés est identique à celui des rectangles. En effet, dans le cas de polygones réguliers, dont les côtés mesurent exactement la même chose (comme les triangles équilatéraux), il suffira de multiplier la longueur d’un côté par le nombre de côtés de la figure :
- Carré. 4 côtés identiques qui mesurent a, donc P = ax 4 .
- Triangle équilatéral . 3 côtés identiques qui mesurent b, donc P = bx 3 .
Il en va de même pour les autres figures similaires, quel que soit leur nombre de faces. Par contre, pour les triangles isocèles et scalènes, il faut additionner chaque longueur de chaque côté.
Périmètre d’un polygone irrégulier

Dans le cas de polygones irréguliers, c’est-à-dire ceux qui n’ont pas des côtés et des angles identiques , il suffira d’ additionner les mesures de tous les côtés du polygone , quelle que soit sa forme. Si nous n’avons pas les mesures de certains de ces côtés, la tâche sera compliquée car nous devons d’abord les calculer, mais ensuite nous pouvons procéder à leur addition sans aucune difficulté.
Continuer avec : Polyèdres







