Nous expliquons ce qu’est le plan cartésien, comment il a été créé, ses quadrants et ses éléments. Aussi, comment les fonctions sont représentées.
Qu’est-ce que le plan cartésien ?
Un plan cartésien ou un système cartésien est appelé un diagramme de coordonnées orthogonales utilisé pour les opérations géométriques dans l’espace euclidien (c’est-à-dire l’espace géométrique qui répond aux exigences formulées dans l’Antiquité par Euclide).
Il est utilisé pour représenter graphiquement des fonctions mathématiques et des équations de géométrie analytique . Il permet également de représenter des relations de mouvement et de position physique.
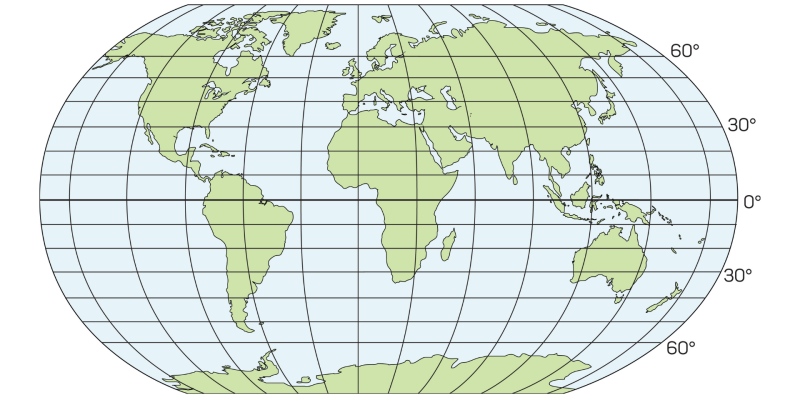
C’est un système bidimensionnel, composé de deux axes qui s’étendent d’une origine à l’infini (formant une croix). Ces axes se coupent en un seul point (indiquant le point d’origine des coordonnées ou le point 0,0).
Un ensemble de marques de longitude sont dessinées sur chaque axe , qui servent de référence pour localiser des points, dessiner des chiffres ou représenter des opérations mathématiques . En d’autres termes, c’est un outil géométrique pour mettre ces derniers en relation graphiquement.
Le plan cartésien porte le nom du philosophe français René Descartes (1596-1650), créateur du domaine de la géométrie analytique .
Voir aussi : Angle
Histoire du plan cartésien

Le plan cartésien était une invention de René Descartes , comme nous l’avons dit, un philosophe central dans la tradition occidentale . Sa perspective philosophique a toujours été basée sur la recherche du point d’origine de la connaissance .
Dans le cadre de cette recherche, il a mené des études approfondies sur la géométrie analytique, dont il est considéré comme le père et le fondateur. Il a réussi à transférer mathématiquement la géométrie analytique au plan bidimensionnel de la géométrie plane et a donné naissance au système de coordonnées que nous utilisons et étudions encore aujourd’hui.
A quoi sert le plan cartésien ?

Le plan cartésien est un schéma dans lequel on peut localiser des points, en fonction de leurs coordonnées respectives sur chaque axe, comme le fait un GPS sur le globe. A partir de là, il est également possible de représenter graphiquement le mouvement (le déplacement d’un point à un autre dans le système de coordonnées).
De plus, il vous permet de dessiner des figures géométriques bidimensionnelles à partir de lignes et de courbes. Ces chiffres correspondent à certaines opérations arithmétiques , telles que des équations, des opérations simples, etc.
Il y a deux façons de résoudre ces opérations : mathématiquement puis graphiquement, ou on peut trouver une solution graphiquement, puisqu’il y a une correspondance claire entre ce qui est illustré sur le plan cartésien, et ce qui est exprimé en symboles mathématiques.
Dans le système de coordonnées, pour localiser les points , nous avons besoin de deux valeurs : la première correspondant à l’axe horizontal X et la seconde à l’axe vertical Y , qui sont notées entre parenthèses et séparées par une virgule : (0,0) par exemple, est le point d’intersection des deux droites.
Ces valeurs peuvent être positives ou négatives, selon leur emplacement par rapport aux lignes qui composent le plan.
Quadrants du plan cartésien

Comme nous l’avons vu, le plan cartésien est constitué par l’intersection de deux axes de coordonnées, c’est-à-dire de deux droites infinies, repérées par les lettres x (horizontale) et d’autre part y (verticale). Si nous les regardons, nous verrons qu’ils forment une sorte de croix, divisant ainsi le plan en quatre quadrants, qui sont :
- Quadrant I. Dans la région supérieure droite, où les valeurs positives peuvent être représentées sur chaque axe de coordonnées. Par exemple : (1,1).
- Quadrant II. Dans la région supérieure gauche, où les valeurs positives peuvent être représentées sur l’axe des y mais négatives sur l’ axe des x . Par exemple : (-1, 1).
- Quadrant III. Dans la région inférieure gauche, où les valeurs négatives peuvent être représentées sur les deux axes. Par exemple : (-1,-1).
- Quadrant IV. Dans la région inférieure droite, où les valeurs négatives peuvent être représentées sur l’axe des y mais positives sur l’ axe des x . Par exemple : (1, -1).
Éléments du plan cartésien
Le plan cartésien est composé de deux axes perpendiculaires, comme nous le savons déjà : les ordonnées ( axe y ) et les abscisses ( axe x ) . Les deux lignes s’étendent à l’infini, à la fois dans leurs valeurs positives et négatives. Le seul point de croisement entre les deux est appelé l’origine (coordonnées 0,0) .
En partant de l’origine, chaque axe est marqué de valeurs exprimées en nombres entiers. Le point d’intersection de deux points quelconques est appelé un point. Chaque point est exprimé dans ses coordonnées respectives , en disant toujours d’abord l’abscisse puis l’ordonnée. En joignant deux points, vous pouvez construire une ligne et avec plusieurs lignes une figure.
Fonctions sur un plan cartésien

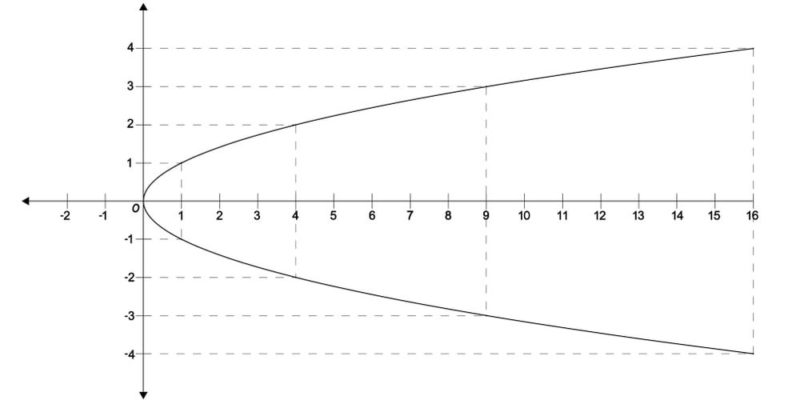
Les fonctions mathématiques peuvent être exprimées graphiquement sur un plan de coordonnées , tant que nous exprimons la relation entre une variable x et une variable y de telle manière qu’elle puisse être résolue.
Par exemple, si nous avons une fonction qui indique que la valeur de y sera 4 lorsque la valeur de x est 2, nous pouvons dire que nous avons une fonction exprimable comme ceci : y = 2x. La fonction indique la relation entre les deux axes, et permet de donner une valeur à une variable connaissant la valeur de l’autre .
Par exemple si x = 1, alors y = 2. Par contre, si x = 2, alors y = 4, si x = 3, alors y = 6, etc. En trouvant tous ces points dans le système de coordonnées, nous aurons une ligne droite, puisque la relation entre les deux axes est continue et stable, prévisible. Si nous continuons la ligne droite à l’infini, alors nous savons quelle sera la valeur de x dans tous les cas de y .
La même logique s’appliquera à d’autres types de fonctions, plus complexes, qui renverront des lignes courbes, des paraboles, des figures géométriques ou des lignes pointillées, selon la relation mathématique exprimée dans la fonction. Cependant, la logique restera la même : exprimer la fonction graphiquement en attribuant des valeurs aux variables et en résolvant l’équation.