Nous expliquons ce qu’est l’addition ou l’addition en mathématiques, son histoire, ses propriétés et ses exemples. En outre, les méthodes d’addition de fractions.

Quelle est la somme?
La somme ou l’addition est une opération mathématique fondamentale, qui consiste en l’incorporation de nouveaux éléments à un ensemble numérique , c’est-à-dire la fusion de deux nombres pour en obtenir un nouveau, qui exprime la valeur totale des deux précédents. L’addition est le principe fondamental avec lequel nous apprenons à nous rapporter aux nombres, puisque le simple fait de compter un par un (1, 2, 3, 4…) revient à additionner 1 (1+0, 1+1, 1+2 , 1+3…).
L’addition est une opération de type arithmétique, qui permet de combiner des nombres de différents types : naturel , entier , fractionnaire, réel, rationnel, irrationnel et complexe, ainsi que les structures qui leur sont associées, comme les espaces vectoriels ou les matrices. Dans l’ algèbre moderne , il est représenté par le symbole + , inséré entre les éléments à additionner, et exprimé verbalement par « plus » : « 1 + 1 = 2 » se lit « un plus un égale deux ».
D’autre part, les éléments à additionner sont appelés « additions », et le nombre obtenu à la fin est appelé le « résultat ».
Cela peut vous aider : Mathématiques
histoire d’addition
L’addition est l’une des opérations mathématiques les plus anciennes et les plus élémentaires connues. On pense que l’ être humain néolithique maniait déjà des principes mathématiques élémentaires , parmi lesquels figureraient nécessairement l’addition et la soustraction, puisque ces opérations sont faciles à démontrer face à des provisions agricoles qui augmentaient et diminuaient selon la période de l’année.
Cependant, l’étude de l’addition et de son application aux nombres tant naturels que fractionnaires a commencé avec les anciens Égyptiens , et a continué à se développer dans des aspects plus complexes avec les Babyloniens, et surtout les Chinois et les Hindous, qui ont été les premiers à additionner des nombres négatifs. Mais il faudra attendre la Renaissance pour que l’essor de la banque impose l’ajout des décimales et des logarithmes vulgaires.
Propriétés supplémentaires
L’addition en tant qu’opération mathématique a un ensemble de propriétés, qui sont :
- propriété commutative . Il établit que l’ordre des additions ne modifie pas le résultat, c’est-à-dire que a + b est exactement le même que b + a, et dans les deux cas le même résultat est obtenu.
- Propriété associative . Il établit que lors de l’addition de trois éléments ou plus, il est possible d’en regrouper deux pour les résoudre en premier, quels qu’ils soient, sans altérer le résultat final. Autrement dit, si nous voulons ajouter a + b + c, nous pouvons choisir entre deux chemins : (a + b) + c ou a + (b + c), sans affecter du tout le résultat.
- Propriété d’identité . Il indique que zéro est un élément neutre dans l’opération, donc l’ajouter à n’importe quel autre nombre donnera toujours ce dernier nombre : a + 0 = a.
- propriété de clôture . Il établit que le résultat d’une somme appartiendra toujours au même ensemble numérique des additions, à condition que celles-ci partagent à leur tour le même ensemble. Autrement dit, si les additions a et b appartiennent à N (naturel), Z (entier), Q (irrationnel), R (réel) ou C (complexe), le résultat de l’addition appartiendra également au même ensemble.
Exemples de somme
Voici quelques exemples d’ajouts simples :
- Une femme a quatre fleurs, mais c’est son anniversaire et on lui en donne huit de plus. Combien y a-t-il de fleurs en fin de journée ? 4 fleurs + 8 fleurs = 12 fleurs.
- Un berger a 15 moutons, tandis que son collègue en a 13. S’ils décident de fusionner leurs troupeaux, combien de moutons auront-ils en tout ? 15 moutons + 13 moutons = 28 moutons.
- Un pommier donne à son propriétaire 5 pommes par mois. Combien de pommes aura-t-il à la fin d’une année ? Comme une année est de 12 mois, il faut additionner 5 douze fois, en appliquant la propriété associative : (5 + 5) + (5 + 5) + (5 + 5) + (5 + 5) + (5 + 5) + ( 5 + 5) = (10 + 10) + (10 + 10) + (10 + 10) = 20 + 20 + 20 = 60 pommes par an.
addition de fractions
Lorsqu’il s’agit d’additionner des fractions, il existe différentes méthodes que nous pouvons appliquer pour obtenir le résultat, selon qu’il s’agit de fractions propres, impropres et mixtes.
- Méthode pour additionner des fractions avec le même dénominateur . C’est le cas le plus simple, où nous additionnons simplement les numérateurs et gardons le même dénominateur. Par exemple:
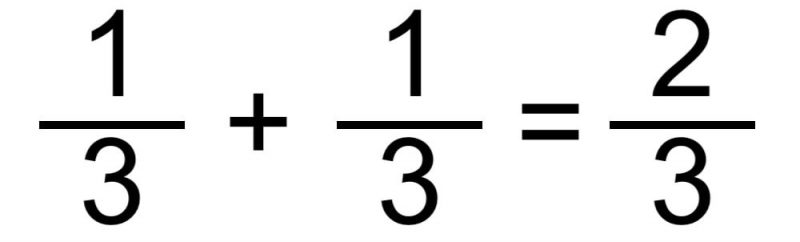
ou
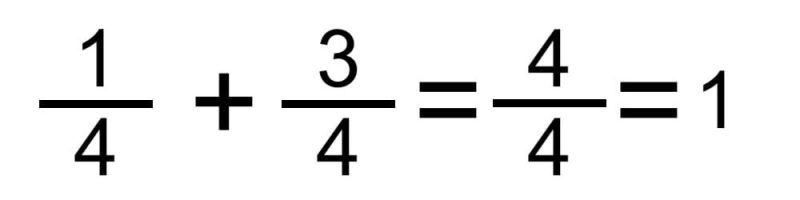
- méthode papillon . Cette méthode nous permet d’ajouter n’importe quel type de fractions avec différents dénominateurs, simplement en multipliant le numérateur du premier par le dénominateur du second et vice versa, puis en additionnant les produits (pour obtenir le numérateur), puis en multipliant les dénominateurs pour obtenir le dénominateur de la fraction finale. Une fois ces opérations effectuées, nous devrons souvent réduire le résultat. Par exemple:
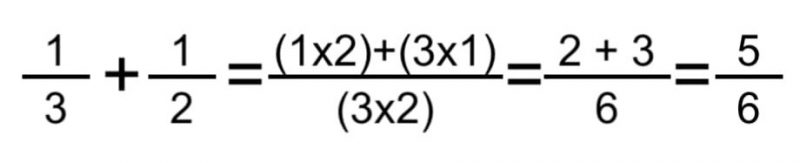
- Méthode d’addition de trois fractions . Dans ce cas, nous additionnons simplement les deux premiers et ajoutons le dernier au résultat, en appliquant la méthode précédente et en réduisant ou en simplifiant le résultat si nécessaire. Par exemple:
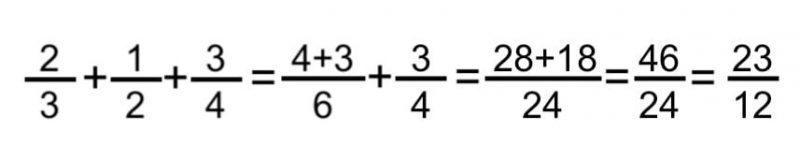
Continuer avec : Feuille de calcul







