Système binaire

Nous expliquons ce qu’est le système binaire, comment il fonctionne, ses applications et d’autres fonctionnalités. De plus, des exercices résolus.

Dans le système binaire, tous les nombres sont représentés par deux chiffres.

Qu’est-ce que le système binaire ?

Le système binaire ou système dyadique est un système de numérotation fondamental en informatique et en informatique , dans lequel tous les nombres peuvent être représentés à l’aide de chiffres composés de combinaisons de deux chiffres uniques.

Dans le cas du code binaire, les chiffres utilisés sont des zéros (0) et des uns (1) . Il ne faut pas confondre le système avec le code , puisque le premier pourrait fonctionner avec des chiffres comme a et b (puisque la logique est la même), tandis que le second fonctionne spécifiquement avec 1 et 0.

Le code binaire est fondamental pour la construction des ordinateurs que nous connaissons aujourd’hui, notamment parce qu’il s’adapte bien à la présence ou à l’absence de tensions électriques , donnant ainsi lieu à un peu d’ information : présent ou absent, c’est-à-dire 1 ou 0, respectivement.

Cependant, le code binaire n’a pas été inventé exclusivement pour le monde informatique. Déjà dans l’Antiquité orientale, de nombreux mathématiciens comme l’Hindou Pingala (c. IIIe ou IVe siècle av. J.-C.) l’avaient proposé, coïncidant dans de nombreux cas avec l’invention du nombre 0.

En effet, les livres oraculaires comme le I Ching sont composés selon leur propre code, ordonnant leurs hexagrammes en séries équivalentes à 3 « bits ». Plus tard, le philosophe chinois Shao Yong (1011-1077) les ordonna selon une méthode binaire.

Pour sa part, le système binaire moderne est l’œuvre du philosophe allemand Gottfried W. Leibniz (1646-1716). Plus tard, en 1854, le mathématicien britannique George Boole (1815-1864), détailla l’algèbre booléenne, fondamentale dans le développement du système binaire actuel dans les circuits électroniques.

Les premières tentatives de mise en pratique de ce système furent les travaux des Américains Claude Shannon (1916-2001) et George Stibitz (1904-1995) en 1937.

Voir aussi : Programmation

Comment fonctionne le système binaire ?

Le système binaire fonctionne sur la base de la représentation de toute information au moyen de deux chiffres . En code binaire, ils sont 0 et 1, mais ils pourraient bien être n’importe quoi, tant qu’ils sont identiques et représentent la même chose : une opposition binaire, comme oui ou non, haut ou bas, allumé ou éteint.

Ainsi, ce code permet « d’écrire » des informations au moyen d’éléments physiques similaires : la polarité d’un disque magnétique (positive ou négative), la présence ou l’absence de tension électrique, etc.

Par conséquent, le système binaire permet à n’importe quelle lettre ou valeur décimale d’être « traduite » en une séquence binaire, et permet même d’effectuer des opérations arithmétiques et autres.

Par exemple, la lettre A dans le code binaire représente 1010, tandis que le chiffre 1 représente 0001. Dans d’autres codes, cette même information pourrait être représentée en binaire comme abab et bbba , ou +++ * et ***+ , par exemple.

Ainsi, selon le code binaire, le mot etcetera serait représenté comme ceci :

01100101 (e)
01110100 (t)
01100011 (c)
11000011 (e)
10101001 (´)
01110100 (t)
01100101 (e)
01110010 (r)
01100001 (a)

Caractéristiques du système binaire

Les valeurs d’un système binaire peuvent être n’importe quoi, comme on et off.

Le système binaire est caractérisé par ce qui suit :

Il utilise deux unités (1 et 0 dans le cas du code binaire) pour représenter des informations spécifiques à travers des séquences spécifiques de ces chiffres. Il doit toujours y en avoir deux, avec des valeurs totalement distinguables et mutuellement exclusives (il ne peut y avoir 1 et 0 en même temps).
Il représente la base des systèmes informatiques et de calcul , dans lesquels une séquence de huit bits constitue un octet d’information, correspondant à une lettre, un chiffre ou un caractère.
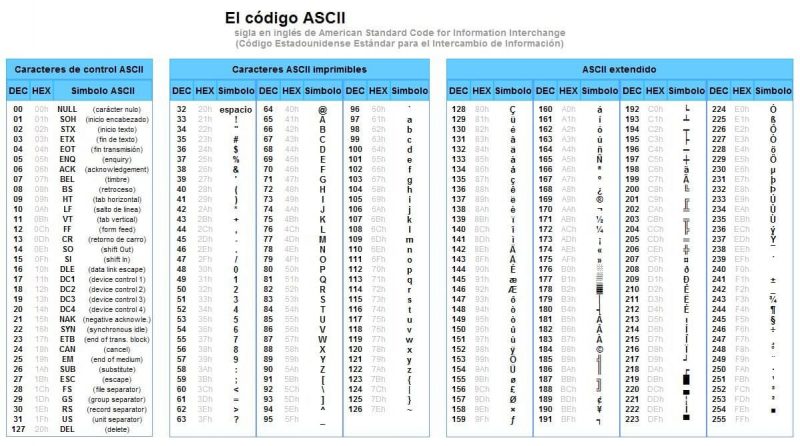
Il permet de traduire toutes les données exprimées en notation décimale, hexadécimale ou octale, entre autres systèmes de notation d’information ( ASCII , etc.).
Il permet la lecture de conditions réelles et de matériaux dont les états physiques peuvent être l’un ou l’autre : polarité magnétique, tension, etc.