Nous vous expliquons ce qu’est la loi de la gravitation universelle, comment est sa formule et son énoncé. Aussi, des exemples d’utilisation de votre formule.
Qu’est-ce que la loi de la gravitation universelle ?
La loi de la gravitation universelle est l’une des lois physiques formulées par Isaac Newton dans son livre Philosophiae Naturalis Principia Mathematica de 1687. Elle décrit l’interaction gravitationnelle entre des corps massifs , et établit une relation de proportionnalité de la force gravitationnelle avec la masse des corps. .
Pour formuler cette loi, Newton en déduit que la force avec laquelle deux masses s’attirent est proportionnelle au produit de leurs masses divisé par la distance qui les sépare au carré. Ces déductions sont le résultat d’une vérification empirique par l’ observation .
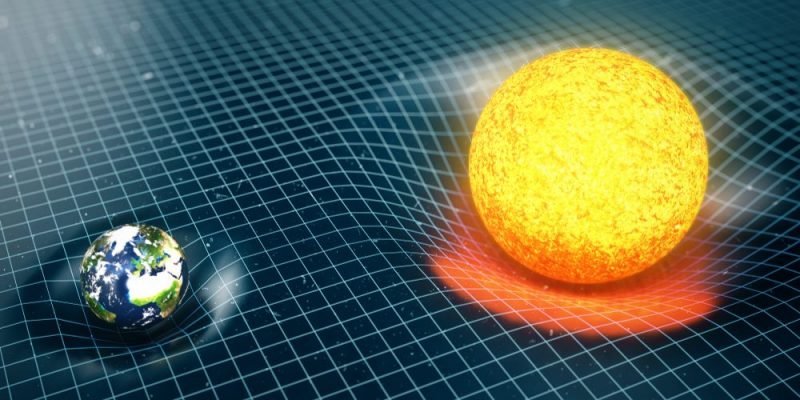
La loi implique que plus deux corps sont proches et massifs, plus ils s’attirent fortement . Comme d’autres lois newtoniennes, elle représentait à l’époque un bond en avant dans les connaissances scientifiques .
Or, on sait aujourd’hui qu’à partir d’une certaine quantité de masse, cette loi perd sa validité (dans le cas des objets supermassifs), et il faut travailler avec la Loi de la Relativité Générale formulée en 1915 par Albert Einstein. La loi de la gravitation universelle est alors une approximation de la loi d’Einstein mais elle est tout de même utile pour comprendre la plupart des phénomènes gravitationnels du système solaire .
Cela peut vous aider : Méthode scientifique
Énoncé de la loi de la gravitation universelle
L’énoncé formel de cette loi newtonienne stipule que :
» La force avec laquelle deux objets s’attirent est proportionnelle au produit de leurs masses et inversement proportionnelle au carré de la distance qui les sépare . »
Cela signifie que deux corps quelconques s’attirent avec une force plus ou moins grande selon que leur masse est plus ou moins grande et selon la distance qui les sépare.
Formule de la loi de la gravitation universelle
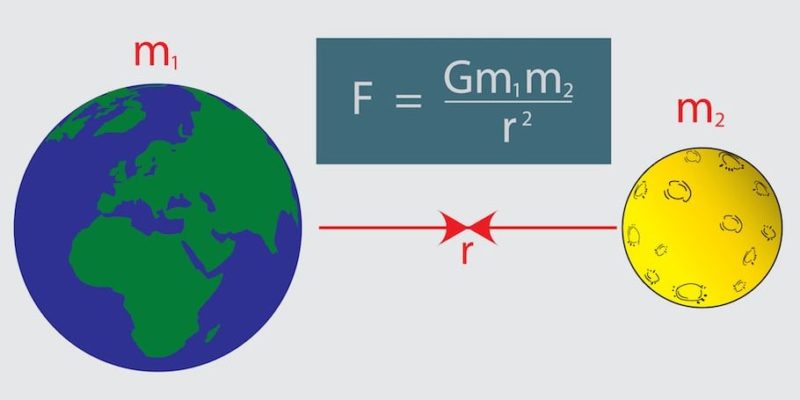
La formule fondamentale de la loi de la gravitation universelle est la suivante :
F = | (G . m 1 . m 2 ) / r² | . r*
Où:
- F est la force d’attraction entre deux masses
- G est la constante gravitationnelle universelle ( 6.673484.10 -11 Nm 2 /kg 2 )
- m 1 est la masse de l’un des corps
- m 2 est la masse d’un autre des corps
- r la distance qui les sépare.
- r* est le vecteur unitaire indiquant la direction de la force.
Si les forces d’attraction de chaque corps sont calculées (la force que la masse 1 exerce sur la masse 2 et vice versa), il y aura deux forces égales en amplitude et dans des directions opposées. Pour obtenir cette différence de signe, il faut écrire l’équation comme suit :
F12 = | G. m 1 .m 2 / (r1 1 -r 2 ) 3 | . ( r1 – r2 )
En changeant 1 par 2, nous obtenons la force pour chaque cas. Écrit de cette façon, le vecteur (r 1 -r 2 ) donne la bonne direction ( signe) pour chaque force.
Exemples de la loi de la gravitation universelle
Résolvons quelques exercices comme exemple d’application de cette formule.
- Supposons qu’une masse de 800 kg et une masse de 500 kg s’attirent dans le vide, séparées par un espace de 3 mètres. Comment calculer la force d’attraction qu’ils subissent ?
En appliquant simplement la formule :
F = G. (m 1 .m 2 )/r 2
Soit : F = (6,67.10 -11 Nm 2 /kg 2 ) . (800kg . 500kg) / (3m) 2
Et alors : F = 2,964 x 10 -6 N.
- Autre exercice : A quelle distance doit-on placer deux corps d’une masse de 1 kg , pour qu’ils s’attirent avec une force de 1 N ?
Partant de la même formule
F = G. (m 1 .m 2 )/r 2
Nous allons effacer la distance en restant que r 2 = G.(m 1 .m 2 )/ F
Ou ce qui revient au même : r = √ (G.[m 1 .m 2 ])/ F
Soit : r = √ (6,67×10 -11 Nm 2 /kg 2 . 1kg x 1kg) / 1N
Le résultat est que r = 8,16 x 10 -6 mètres.
Continuer avec : Champ gravitationnel