Nous expliquons ce qu’est une fonction mathématique, comment elle peut être exprimée, ses variables, les types qui existent et d’autres caractéristiques.
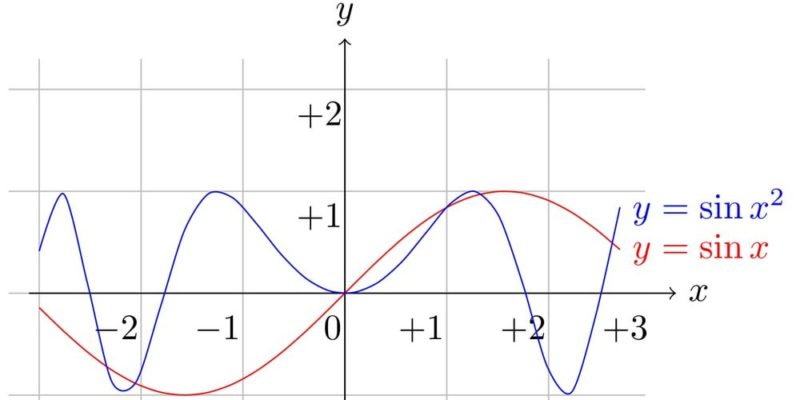
Qu’est-ce qu’une fonction mathématique ?
Une fonction mathématique (également appelée simplement fonction) est la relation entre une grandeur et une autre , lorsque la valeur de la première dépend de la seconde.
Par exemple, si nous disons que la valeur de la température du jour dépend de l’heure à laquelle nous la consultons, nous établirons sans le savoir une fonction entre les deux choses. Les deux grandeurs sont des variables , mais elles se distinguent entre :
- Variable dépendante. C’est celle qui dépend de la valeur de l’autre grandeur. Dans le cas de l’exemple, il s’agit de la température.
- Variable indépendante. C’est celui qui définit la variable dépendante. Dans le cas de l’exemple c’est l’heure.
Ainsi, toute fonction mathématique consiste en la relation entre un élément d’un groupe A et un autre élément d’un groupe B, tant qu’ils sont liés de manière unique et exclusive. Par conséquent, ladite fonction peut être exprimée en termes algébriques , en utilisant les signes suivants :
f : A → B
un → f(un)
Où A représente le domaine de la fonction ( f ), l’ensemble des éléments de départ, tandis que B est le codomaine de la fonction, c’est-à-dire l’ensemble d’arrivée. Par f(a) on note la relation entre un objet arbitraire a appartenant au domaine A , et le seul objet de B qui lui correspond (son image ).
Ces fonctions mathématiques peuvent également être représentées sous forme d’équations , recourant à des variables et des signes arithmétiques pour exprimer la relation entre les grandeurs. Ces équations, à leur tour, peuvent être résolues, en effaçant leurs inconnues, ou être tracées géométriquement.
Cela peut vous aider: Algèbre
Types de fonctions mathématiques
Les fonctions mathématiques peuvent être classées selon le type de correspondance qui se produit entre les éléments du domaine A et ceux de B, ayant ainsi les éléments suivants :
- fonction injective. Toute fonction sera injective si différents éléments du domaine A correspondent à différents éléments de B , c’est-à-dire qu’aucun élément du domaine ne correspond à la même image d’un autre.
- fonction surjective. De même, on parlera de fonction surjective (ou subjective) lorsque chaque élément du domaine A correspond à une image du domaine B , même si cela implique le partage d’images.
- fonction bijective. Cela se produit lorsqu’une fonction est injective et surjective en même temps, c’est-à-dire lorsque chaque élément de A correspond à un seul élément de B , et qu’il n’y a plus d’images non associées dans le codomaine, c’est-à-dire qu’il n’y a pas d’éléments dans B qui ne correspondent pas à un dans A.
Continuer avec : Géométrie analytique







